3Dプログラミングで使う色々なベクトル計算を直観的に身体に覚えさせてあげますのよ【基礎編】

初めに申し上げておきますわ！

お～っほほほほ！！
よくいらっしゃったわね！迷える子犬ちゃんたち！
この記事では3D空間上のオブジェクトを扱うのに便利なベクトル計算についてまとめたいと思いますのよ！
例えば、「ベクトルの回転」あるいは「面と点との距離」なんていうものに興味があるんじゃないかしら？
ベクトルというのはとてもよく考えられた仕組みで、こういったものが簡単に、たとえあなたのような子犬ちゃんにでも計算できるようになっているのよ。
そして私たちがやりたいと思う大抵のベクトル計算については公式を誰かが作ってくれているものよ。
え？じゃあその公式を使えばいいじゃないか、ですって？

シイイイィィッッット！！！！！！！

そんなだからいつまで経ってもヘボヘボのまんまなんですのよ！
貴族たるもの、いついかなる時でも優雅に、そして鷹揚としていなければなりませんわ。鷹揚としているにはどうすればいいのか。そう、応用ですの！！
覚えた公式をただコピペして使っているだけでは何かあったときに応用できずに鷹揚とできなくなるのですわ！！
Oh you！！応用！！鷹揚！！

でも安心なさい？迷える子犬ちゃんたちを救ってあげるのも淑女の役目というものですわ。
今からあなたたちにみっちりきっちり教えてあげますわ！
それも公式の導出方法ではなく、視覚的かつ直観的に身体に覚えさせてあげますのよ！
直観的に理解してしまえば、公式の導出なんてあとはちょちょいのちょいですの！
よろしくって？では行きますのよ！

基礎的事項の確認

以下、単純化のために2次元ベクトルで考えていきますわ。

ベクトルとは

ベクトルが何かも知らない人なんてここには来ていないでしょうけど、念には念を入れて一応説明しておきますのよ。
ベクトルとは「大きさと向きを持った量」である（presented by Wikipedia）
この一言に尽きますわね。「あっちの方にバーーっと」というのがベクトルですわ。
ただこんな言い方をされても一部の選ばれし人間を除くほとんどの場合は、あっち？どっち？そっち？となるのが関の山ですわ。
だから北に一条、東に三坊、という風にちゃんとした基準となる方向と大きさを決めて、その組み合わせで指定するのが貴族というものですわ。
ベクトルの世界では基準となる方向をX軸方向やY軸方向、大きさを数字(スカラーと呼びますの)で表すといった風に決めていますわ。
f:id:spi_8823:20200525232437p:plain:w250
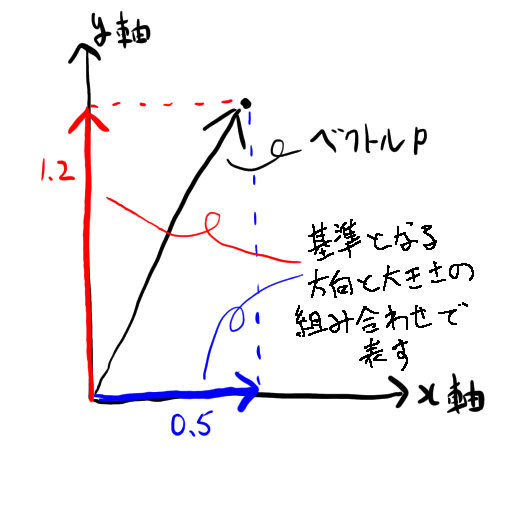
図のようなpというベクトルは数式で $p = \begin{pmatrix} 0.5 \\ 1.2 \end{pmatrix}$ と表されることが多いんですの。
ベクトルを基準となる方向毎に分解したものをベクトルのX成分、Y成分という風に呼ぶことがあるわ。
それぞれベクトルを表す変数に添え字でどの方向に対する成分なのかを書いて、 $p_x$ や $p_y$ といった風に書くことが多いわ。

ベクトルの操作

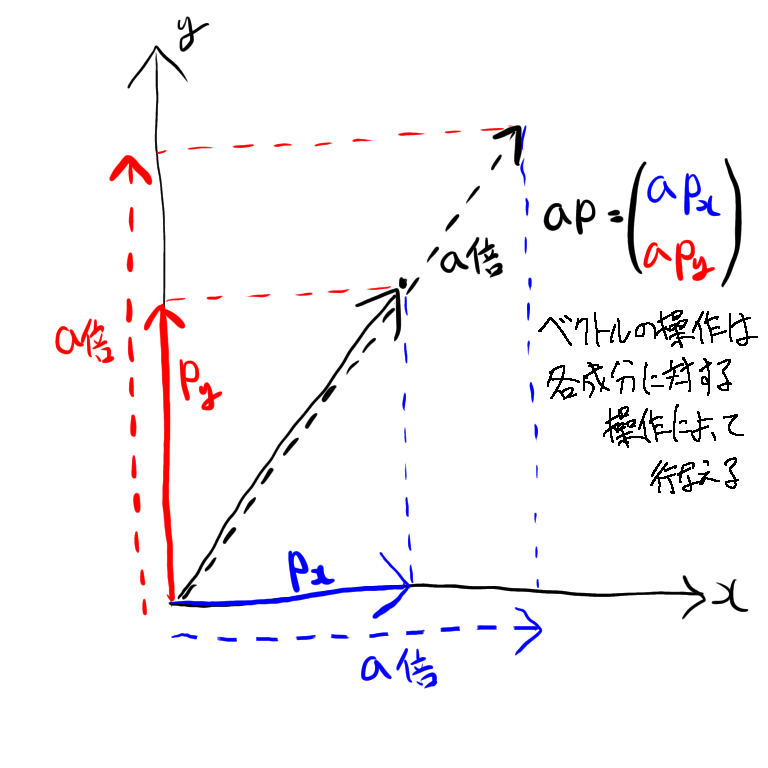
ベクトルに対する操作は、各成分に対する操作に分解できることが多いわ。
例えばベクトルの大きさを $a$ 倍したい場合、 $ap = \begin{pmatrix} ap_x \\ ap_y \end{pmatrix}$ と各成分を $a$ 倍してあげればいいのよ。
f:id:spi_8823:20200526000101p:plain:w250

ベクトルの回転

ベクトルの回転は最も基本的なベクトル操作の一つですわ。
その中でも「ある単位ベクトルがX軸方向を向くように回転させる」方法を理解しておけば応用が利きますのよ。頑張りなさい？
回転させる前のベクトルを $p = \begin{pmatrix} p_x \\ p_y\end{pmatrix}$ としますわよ？
これ各成分 $\begin{pmatrix} p_x \\ 0\end{pmatrix}$ , $\begin{pmatrix} 0 \\ p_y\end{pmatrix}$ を辺に持つ長方形の対角線だと考えると、ベクトルの回転はこの長方形を回転させる操作だと考えることができるわね。
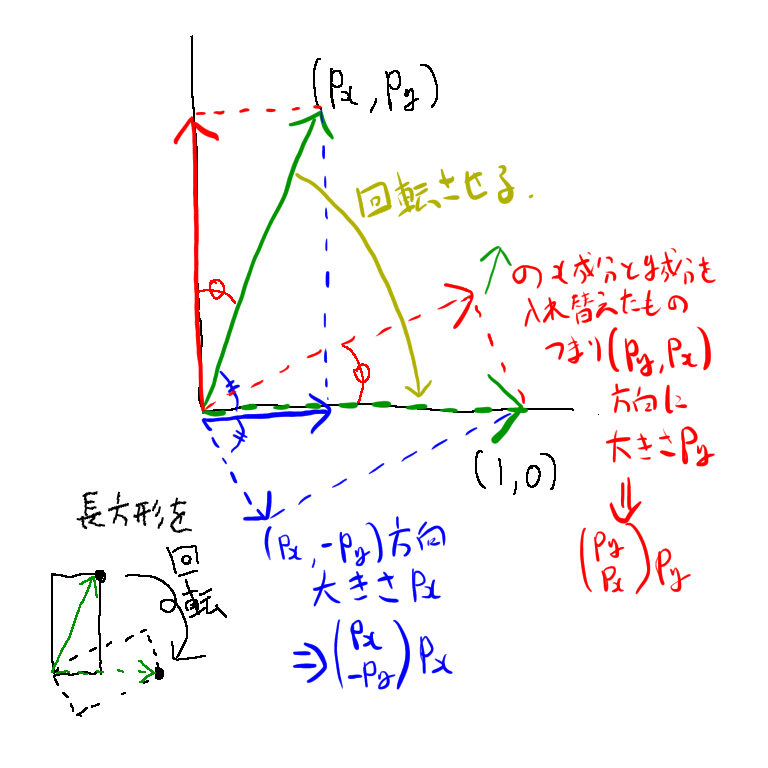
ここで各ベクトル同士の角度関係を考えると、回転によって長方形の各辺は次のように移動するわ。
イメージをつかみやすいように、下の図と一緒に見てみるとよいのですわ。

回転前の長方形にとってのX軸方向　→　ベクトル $p$ のY成分がマイナスになった方向

　　　　　 $\begin{pmatrix} p_x \\ 0\end{pmatrix}$ $=> p_x *$ $\begin{pmatrix} p_x \\ -p_y\end{pmatrix}$

回転前の長方形にとってのY軸方向　→　ベクトル $p$ のX成分とY成分が入れ替わった方向

　　　　　 $\begin{pmatrix} 0 \\ p_y\end{pmatrix}$ $=> p_y *$ $\begin{pmatrix} p_y \\ p_x\end{pmatrix}$
というわけで、「ベクトル $p$ 方向からX軸方向への回転」を「各成分ベクトルの回転に分解」することができたわね。
そして、長方形を回転させるために各辺を回転させるという操作は、 $p$ じゃなくても任意のベクトルに当てはめることができるわ。

したがって同じ方法を使って、別のベクトル $q$ に対して、ベクトル $p$ をX軸方向に回転させるような操作を行うこともできるわ。
　　　　　 $\begin{pmatrix} q_x \\ q_y\end{pmatrix}$ $=> q_x *$ $\begin{pmatrix} p_x \\ -p_y\end{pmatrix}$ $+ q_y *$ $\begin{pmatrix} p_y \\ p_x\end{pmatrix}$
f:id:spi_8823:20200531190958p:plain:w350

式を書くと説明が長くなってしまったのだけれど要するに、

任意のベクトルの回転は、各成分ベクトルの回転に分解することができる
各成分ベクトルの回転は、回転の度合いを表すベクトルの成分を一部マイナスにしたり、X成分とY成分を入れ替えたものをかけることで実現できる

と言えば直観的に理解できるんじゃないかしら？

内積

内積とは、2つのベクトル $p, q$ があったとき、 $p$ を $q$ 方向と $q$ に直角な方向の成分に分解して $q$ 方向成分の大きさを求めるという計算ですわ。
（厳密に言えばこれは $q$ が単位ベクトルだった場合の説明ですわ。そうでない場合、 $q$ 方向成分の大きさに $q$ の大きさだけかけたものが求まりますわ）
演算子はドットで表され、次のような式になりますの。
　　　　　 $p \cdot q = \begin{pmatrix} p_x \\ p_y\end{pmatrix} \cdot \begin{pmatrix} q_x \\ q_y\end{pmatrix} = p_x q_x + p_y q_y$
言い換えれば、ベクトル $p$ の先端からベクトル $q$ の線分上に垂線を下した交点と原点との長さを求めていることになりますわね。
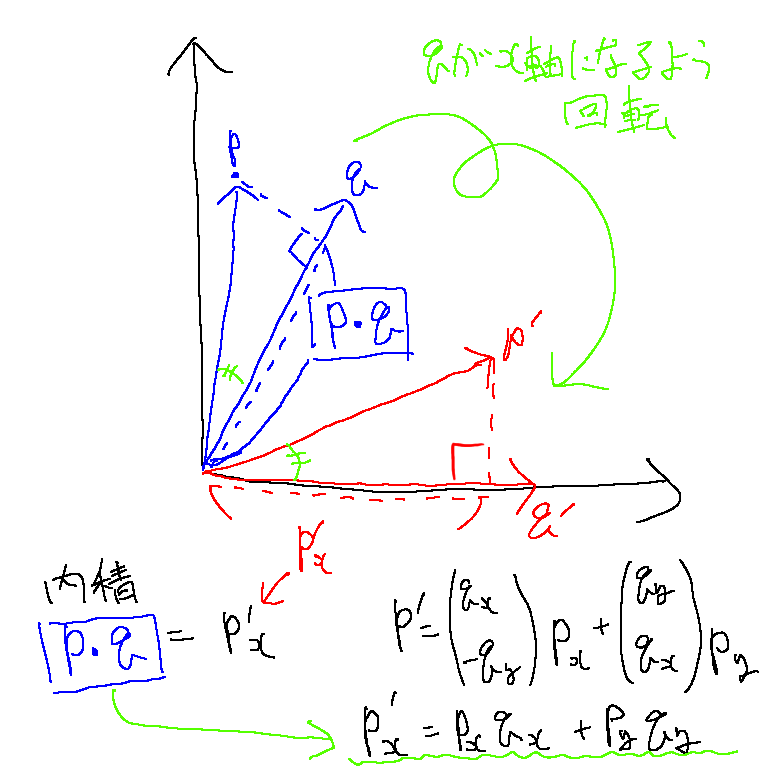
ただし、任意のベクトル $p$ と $q$ を考えてしまうとどうしても話がややこしくなるから、両方に対してベクトル $q$ をX軸まで回転させるような操作をしてから考えれば、あとはベクトル $p'$ の先端からX軸に対して垂線を下した交点と原点との距離、つまり $p'$ のX成分を求めるという話に単純化することができるわ。
これまた具体的なイメージは下の図を見なさい。
そしてこれは「ベクトルの回転」でやった内容と全く同じ操作をしてX成分だけ抜き取ることになりますのよ。
回転の式の上部分だけを見れば $p_x q_x + p_y q_y$ となっているでしょう？これが内積の値ですのよ。
　　　　　 $\begin{pmatrix} p_x \\ p_y\end{pmatrix} => p_x * \begin{pmatrix} q_x \\ -q_y\end{pmatrix} + p_y * \begin{pmatrix} q_y \\ q_x\end{pmatrix}$
f:id:spi_8823:20200531203038p:plain:w300

内積の要約

要するに、内積とは「あるベクトルを回転させたX成分を求める計算」と考えていいんじゃないかしら？
そしてこれは2つのベクトルが同じような向きを向いているほど大きな値になることから、「2つのベクトルの方向の一致度を表す」と考えてもいいわね。
もちろんこれが数学的に厳密ではないと思うけれど、3Dプログラミングで使うには一番わかりやすい考え方なんじゃないかと思うわ。

外積

外積がベクトルの基礎の中では一番直観的に理解するのが難しいですわね……。
何しろ2次元の図では説明できないのだから、とてもイメージがし辛いわ。

外積とは、2つのベクトル $p, q$ が与えられたとき、どちらのベクトルにも垂直でかつ大きさが $p, q$ を2辺とする平行四辺形の面積であるベクトルを求める計算ですわ。
（ただしこれは3次元の場合で、2次元上では1つのベクトルから1つのベクトルを、4次元上では3つのベクトルから1つのベクトルをというように次元によって計算に必要なベクトルの数が増えていくようですのよ）
演算子はクロス $\times$ で表され、次のような3次元ベクトルの式になりますの。かける順番、引く順番を間違えると正しい値を求められないので注意しなければなりませんわよ。
　　　　　 $p \times q = \begin{pmatrix} p_x \\ p_y \\ p_z\end{pmatrix} \times \begin{pmatrix} q_x \\ q_y \\ q_z\end{pmatrix} = \begin{pmatrix} p_y q_z - p_z q_y \\ p_z q_x - p_x q_z \\ p_x q_y - p_y q_y\end{pmatrix}$

$p, q$ を2辺とする平行四辺形の面積

まずはこちらを考えてみましょう。
実はこれ、内積とよく似た操作を行っているのよ。
$p, q$ をXY平面上に落とし込んだベクトル $\begin{pmatrix} p_x \\ p_y \end{pmatrix}$ と $\begin{pmatrix} q_x \\ q_y\end{pmatrix}$ の各成分同士の計算によって、クロス積のZ成分 $p_x q_y - p_y q_x$ が定められているわね。
これ、どこかで見た記憶はないかしら？
そうよ！えらいわ！「ベクトルの回転」の式の下部分だけ見れば同じような式になっているわね！（正負が入れ替わっているのは計算の順番の関係だから適宜読み替えて頂戴！）
　　　　　 $\begin{pmatrix} p_x \\ p_y\end{pmatrix} => p_x * \begin{pmatrix} q_x \\ -q_y\end{pmatrix} + p_y * \begin{pmatrix} q_y \\ q_x\end{pmatrix}$
つまり、ベクトル $p$ を回転させたY座標を求めている、というわけですわね！
$q$ の大きさが1なら、これはそのまま $p$ と $q$ が成す平行四辺形の大きさを求めていることになるんですのよ！
f:id:spi_8823:20200531212311p:plain:w250

ベクトルに垂直な向き

これが外積の難しいところね。
けど、これも2次元で考えればある程度直観に落とし込むことができるわ。
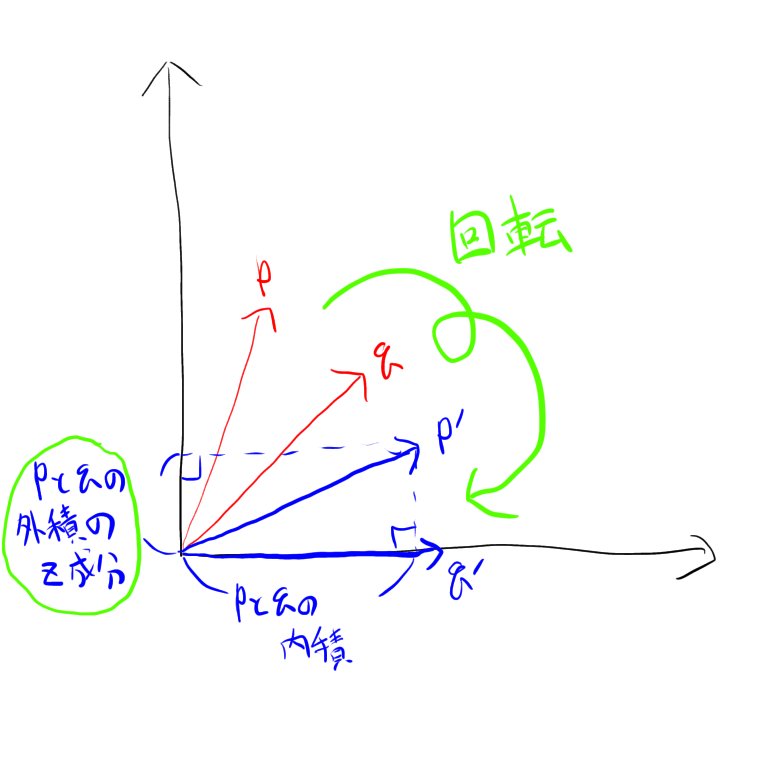
2次元上のベクトルに垂直なベクトルを求めるには「X成分とY成分の比を入れ替えたベクトルを、Y軸(X軸でも可)に対してひっくり返す」という操作を行ってあげればいいのよ。
f:id:spi_8823:20200531213310p:plain:w250
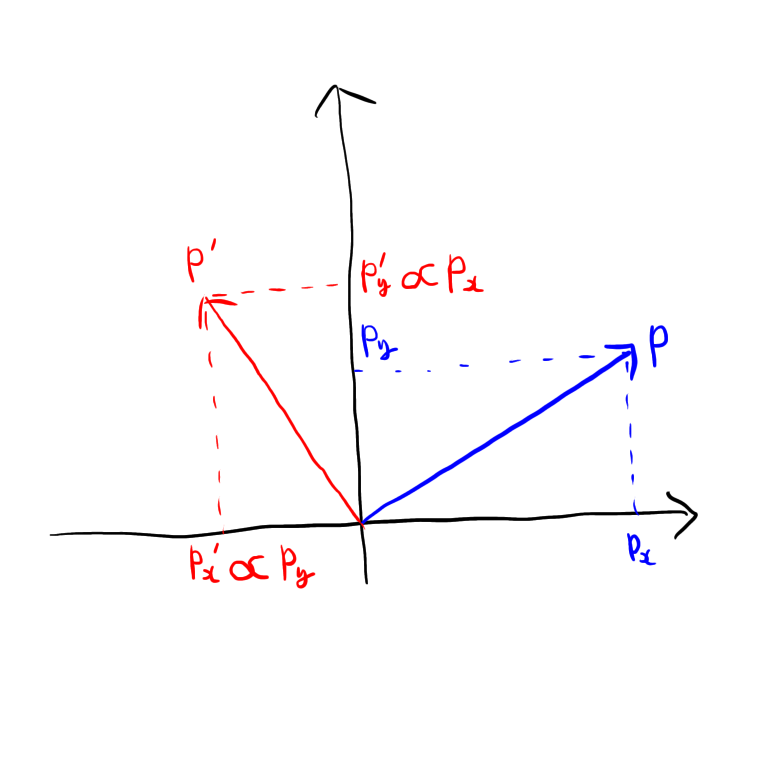
この考え方を3次元にも応用すると、「XY成分、YZ成分、ZX成分の比を入れ替えたベクトルを、Z軸(X軸、Y軸でも可)に対してひっくり返す」という操作になるわ。
「XY成分」と呼んでいるのは、2次元上では軸に対して垂線を引いていたところを、3次元上では面に対して垂線を引く必要があるからね。
そしてXY成分というのがまさに $p, q$ をXY平面上に落とし込んだ時に成す平行四辺形の面積で表されるのよ。この値をZ成分に入れることが「成分の比を入れ替える」という操作になっていますのよ。
そして「軸に対してひっくり返す」という操作の結果、外積の式で表されるような引き算の順番になっているのですわ。

外積の要約

要するに外積とは

各成分に直交する成分を求める（平面上に落とし込んだ2つのベクトルが成す平行四辺形の面積を求める）

求めた直交成分の大きさを、対応する成分の大きさとする（傾きの逆数を求めていると言える）

どれか1つの軸に対してひっくり返す

という操作を行っていると考えるといいんじゃないかしら？
ちょっと2次元から3次元への拡張の部分とか色々おおざっぱな気もするけれど、私の美しい顔に免じて許しなさい！

まとめ

というわけで、ベクトル計算の基礎的な部分について直観的に身体で理解することができたかしら？
何？出来てない？そんなことはありえませんのよ！！ムキーーッ！
というのは冗談で、内積は平行成分を求める計算、外積は直交ベクトルを求める計算という風に覚えておけば後は何とかなると思うわ。
というか正直、内積や外積をこれ以上直観的に理解できる方法があるならぜひとも教えてもらいたいわね！！

お米 is ライス

C#やらUnityやらを勉強していて、これはメモっといたほうがええやろ、ということを書くつもりです